Effiziente Berechnung von K5-Minoren in Graphen
Von Julian Sauer
- 8 Minuten - 1618 WörterEinleitung
Hier geht es um eine etwas umgangssprachlicher formulierte Version meiner Masterarbeit. Wem das nicht akkurat genug ist, der liest sich die Masterarbeit hier durch.
Der Algorithmus basiert auf einem Paper von Kezdy und McGuinness und kann entscheiden, ob ein Graph K5-Minor-frei ist.
Abb. 1: Der K5 ist ein Graph mit 5 Knoten, die untereinander verbunden sind.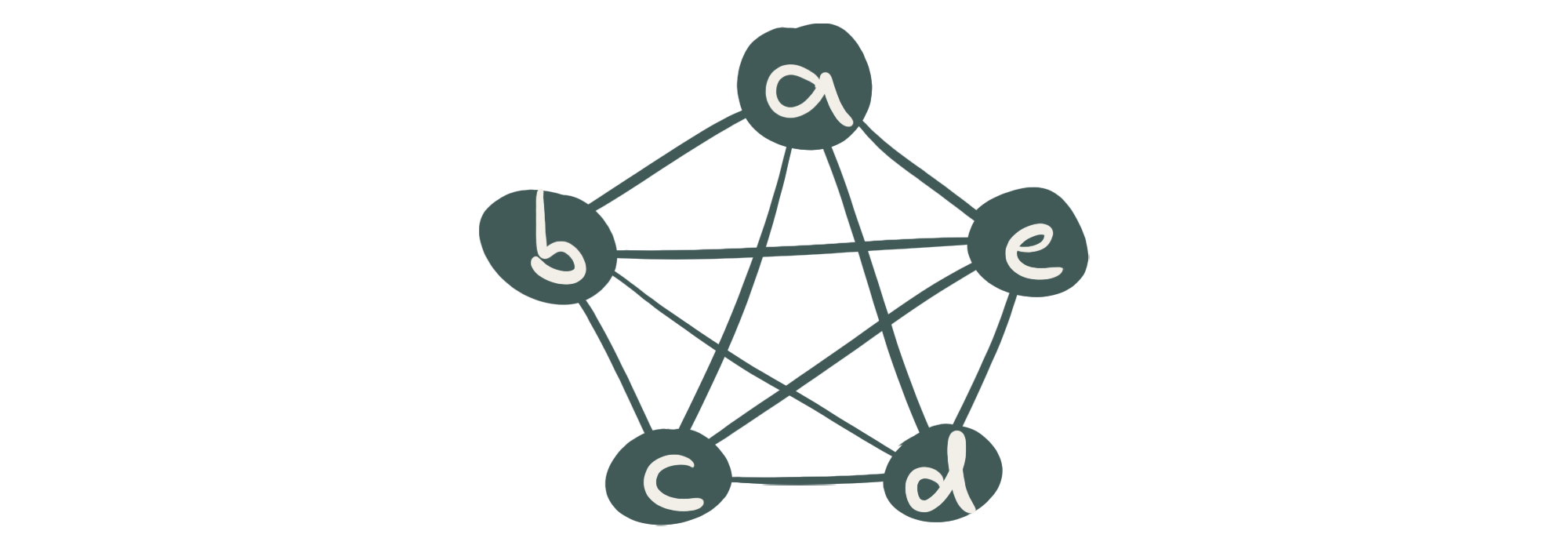
Die Basis für die Berechnung bildet eine Planaritätsprüfung, denn über diese können K5-, leider aber auch K3,3-Minoren gefunden werden. Wird ein K3,3-Minor gefunden, wird dieser entfernt und die Prüfung auf dem dadurch entstehenden Teilgraph wiederholt bis alle Teilgraphen planar sind oder ein K5-Minor gefunden wurde.
Inhaltsverzeichnis
- Graphen, Planarität, Minoren?
- Planaritätsprüfung
- Der Algorithmus von Kezdy & McGuinness
- Sequenzieller Algorithmus zum Finden von K5-Minoren
Graphen, Planarität, Minoren?
Schnell ein paar Begrifflichkeiten erklärt: Ein Graph besteht aus einer Menge von Knoten, die über eine Menge von Kanten paarweise miteinander verbunden sind. Ein Pfad ist eine Menge von aufeinander folgenden Kanten im Graph, die wir durchlaufen können. Beispielsweise besteht beim Haus vom Nikolaus die Herausforderung darin, das Haus durch einen einzelnen Pfad zu zeichnen (kleiner Tipp dazu: Start- und Endpunkt müssen immer die Knoten b und c sein).
Wo wir gerade beim Zeichnen sind: Ein Graph ist dann planar, wenn es eine Möglichkeit gibt, ihn etwa auf einem Blatt Papier zu zeichnen, sodass sich keine Kanten kreuzen.
Das Haus vom Nikolaus ist z.B. planar, weil wir es so zeichnen können:
Abb. 2: Links die bekannte Darstellung vom Haus des Nikolaus. Wenn man beispielsweise die rote Kante umbiegt, wird eine mögliche planare Einbettung deutlich.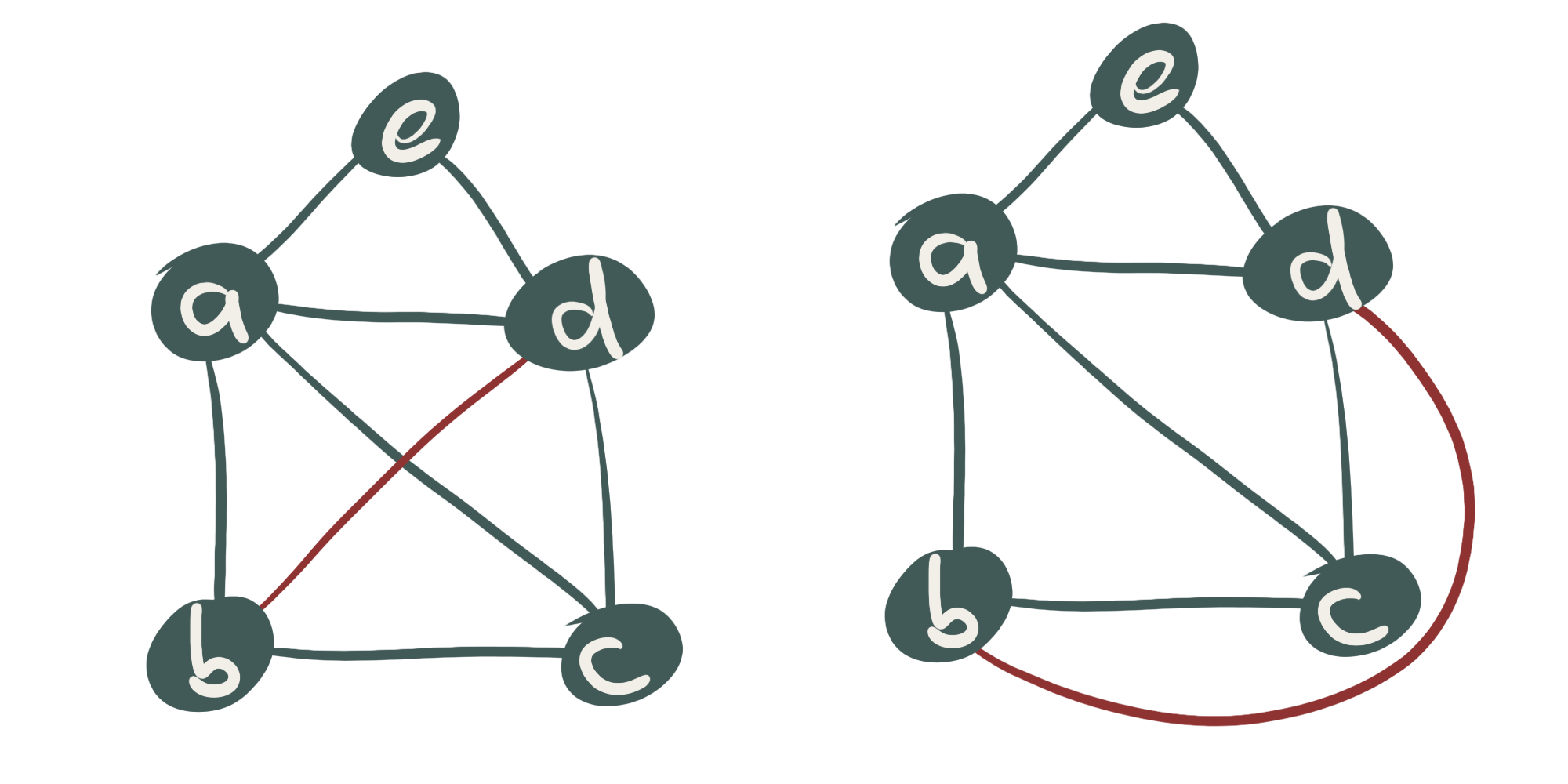
Kuratowski hat festgestellt, dass Graphen dann planar sind, wenn sie keine K5- oder K3,3-Subdivisionen als Teilgraphen enthalten.
Die als K5 bzw. K3,3 bezeichneten Graphen sind die beiden kleinstmöglichen Graphen, die nicht planar sind:
Abb. 3: Links der K5 und rechts der K3,3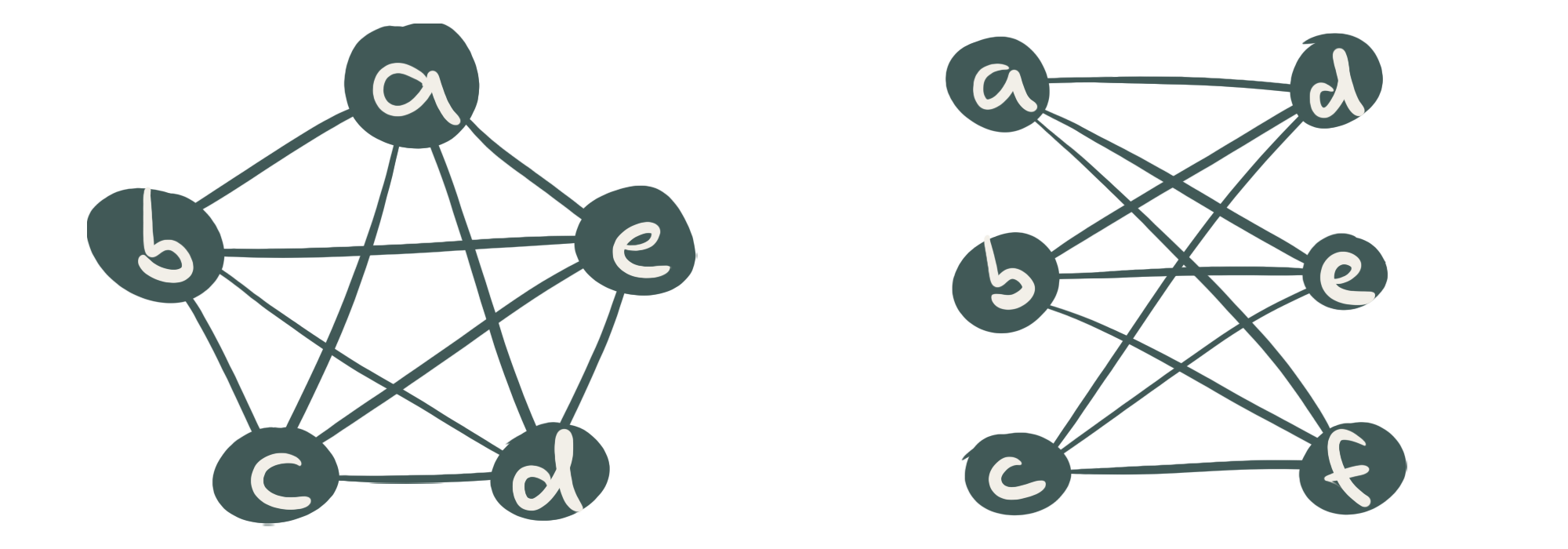
Weil es besser zum Thema passt, nehmen wir allerdings nicht den Satz von Kuratowski, sondern eine äquivalente Formulierung von Wagner: Ein Graph ist planar, wenn er weder einen K5- noch einen K3,3-Minor enthält. Was ist also ein Minor? Es gibt drei Operationen, die wir beliebig oft auf einem Graph anwenden dürfen, um einen Minor daraus zu erzeugen:
- Eine Kante löschen
- Einen Knoten löschen, an dem keine Kanten mehr hängen
- Zwei Knoten verschmelzen, sofern sie mit einer Kante verbunden sind (doppelte Kanten werden entfernt)
Hier eine Animation von Wikipedia, die zeigt, dass der Graph einen K3,3-Minor hat:
Abb. 4: Aus dem Graph wird ein K3,3-Minor erzeugt (Quelle: Wikipedia)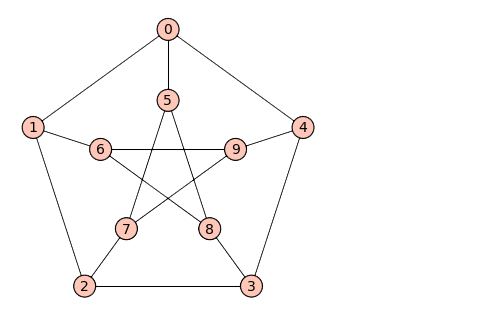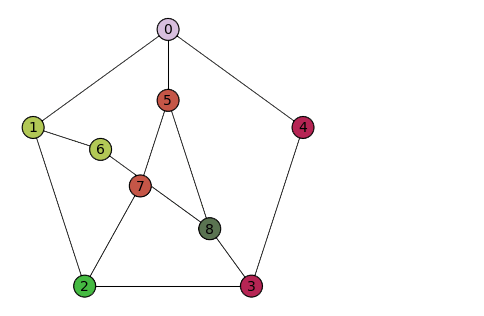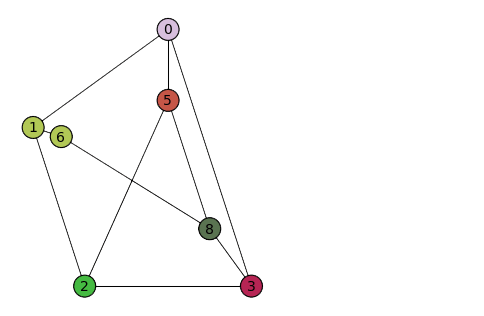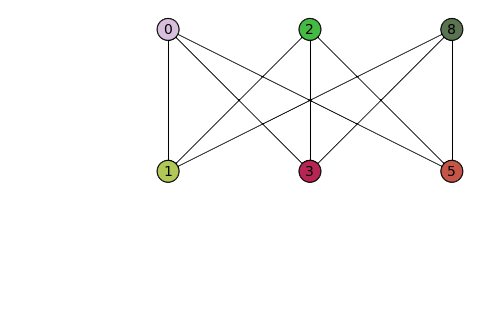
Ungünstiger Weise steigt die Anzahl der möglichen Minoren exponentiell mit der Knoten- und Kantenanzahl. Durch eine Planaritätsprüfung finden wir aber zumindest heraus, ob der Graph planar (K5-Minor-frei) ist oder einen K5-Minor enthält…oder ob er einen K3,3-Minor enthält. Diesen Fall müssen wir später gesondert behandeln.
Planaritätsprüfung
Hopcroft und Tarjan haben bereits 1974 einen Algorithmus vorgestellt, der in linearer Zeit einen Graph auf Planarität prüft und eine planare Darstellung liefern kann.
Im Wesentlichen wird der Graph dafür durch eine Tiefensuche als Baum in der Ebene dargestellt (Bäume sind immer planar).
Alle übrigen Kanten führen zu einem Kreis und können entweder links oder rechts (Abb. 5 ist um 90° gedreht, also oberhalb/unterhalb) am bisher eingebetteten Baum hinzugefügt werden.
Eventuell wechseln diese Kanten beim Hinzufügen weiterer Kanten von links nach rechts oder umgekehrt.
Sobald eine Kante nicht mehr auf diese Art hinzugefügt werden konnte, muss laut dem Theorem von Kuratowski ein K3,3 oder K5 vorliegen.
Andernfalls ist der Graph planar.
Der tatsächliche Algorithmus ist etwas komplexer, für uns ist jedoch lediglich interessant zu wissen, dass wir eine Menge an Knoten und Kanten zurückbekommen, die zu einem nicht-planaren Teilgraph führen.
Abb. 5: Der K3,3 im Planaritätstest. Durch die Tiefensuche wurden alle Knoten mit den Kanten 1 bis 5 gefunden und als Suchbaum dargestellt. Die Kanten 6, 7 und 8 führen zu bereits besuchten Knoten zurück und werden deshalb oberhalb bzw. unterhalb des Baumes eingefügt. Kante 9 muss eine andere Kante kreuzen, da Knoten e durch die Kanten {2, 6, 5, 8} eingeschlossen wird.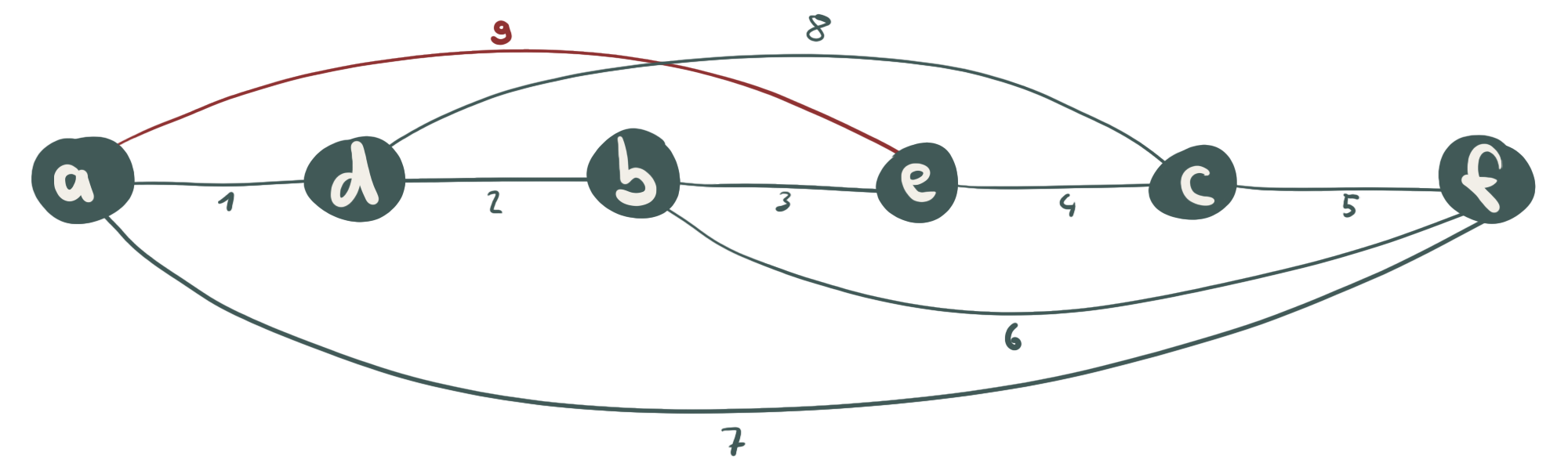
Der Algorithmus von Kezdy & McGuinness
Die Planaritätsprüfung findet also einen K5-Minor, einen K3,3-Minor oder der Graph ist planar.
Wie bereits zuvor festgestellt, können wir im ersten und letzten Fall bereits eindeutig sagen, ob der Graph K5-Minor-frei ist.
Wird dagegen ein K3,3-Minor gefunden, wird dieser entfernt und der Algorithmus rekursiv auf die dadurch entstehenden Minoren angewendet.
Das funktioniert grundlegend so, dass wir ein paar Knoten des K3,3-Minoren entfernen, damit wir bei der erneuten Planaritätsprüfung nicht noch einmal darüber stolpern.
Wir sorgen dafür, dass alle dadurch entstehenden Komponenten nicht nur Minoren unseres ursprünglichen Graphs sind, sondern dass das zusätzlich genau die Minoren sind, die einen K5-Minor enthalten können.
Umgekehrt ist der Graph also K5-Minor-frei, wenn alle seine so erzeugten Minoren K5-Minor-frei sind.
Schauen wir uns also an, wie wir einen K3,3-Minor entfernen können.
Dazu bilden wir augmentierte Komponenten:
Abb. 6: Eine der 3 augmentierten Komponenten zu einem gefunden K3,3-Minor.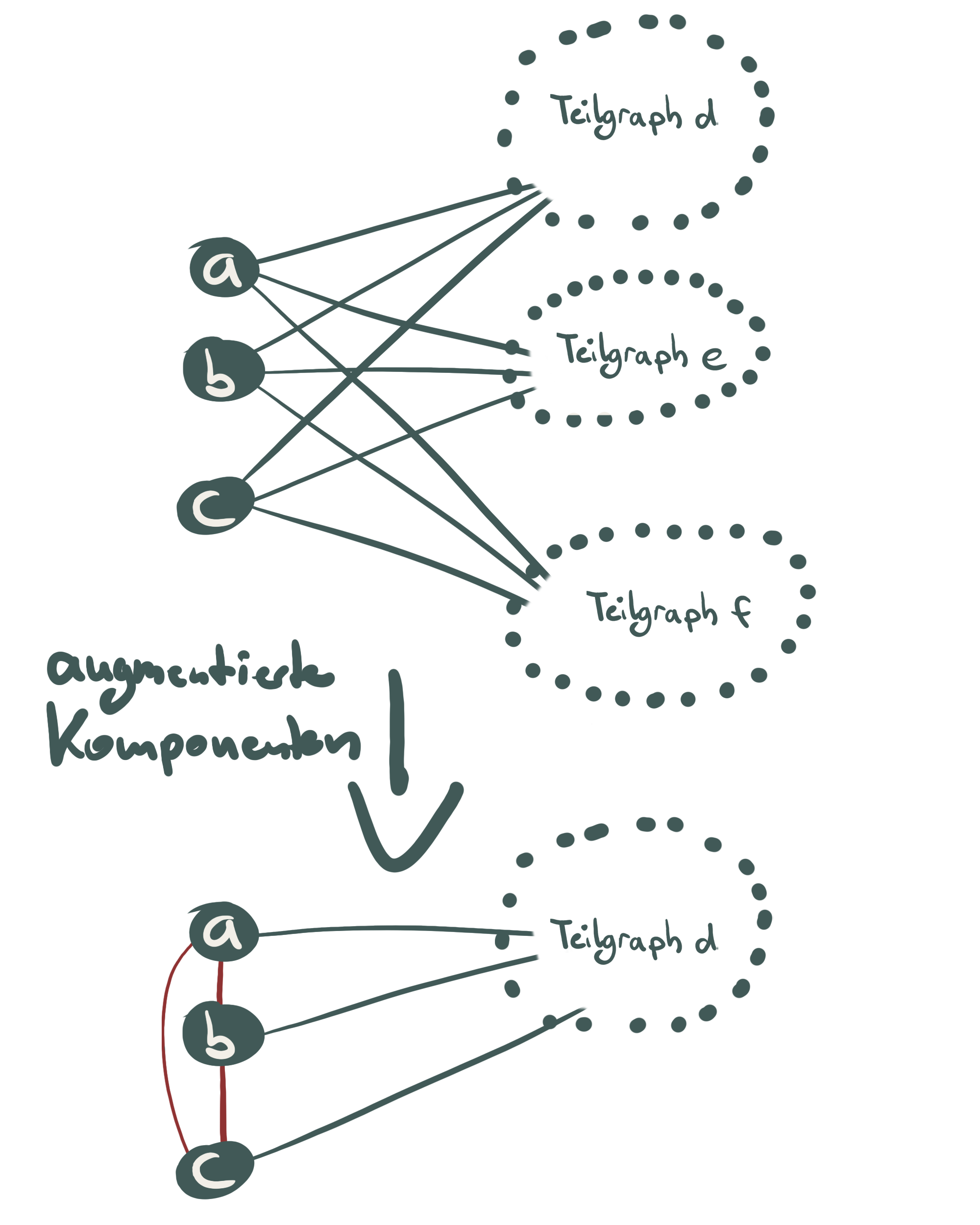
Allgemein werden augmentierte Komponenten für eine Menge an Knoten (im Beispiel a, b und c) wie folgt gebildet:
- Die Knoten werden entfernt, wodurch mehrere voneinander getrennte Komponenten entstehen (die Teilgraphen d, e und f).
- Die entfernten Knoten werden untereinander verbunden (rote Kanten) und anschließend zu jedem der Teilgraphen hinzugefügt.
Wenn wir einen Graph durch 3 Knoten in augmentierte Komponenten aufteilen, ist es wichtig, dass dadurch mindestens 3 Komponenten entstehen.
Denn wenn zum Beispiel die Knoten a, b und c entfernt werden, der Graph danach aber nicht in 3 getrennte Teilgraphen zerfällt und das gleiche für den Fall eintritt, wenn wir die Knoten d, e und f entfernen, dann können wir aus dem gefundenen K3,3-Minor mit den zusätzlichen Pfaden einen K5-Minor bilden:
Abb. 7: Ein K3,3 mit zwei zusätzlichen Kanten. Werden die roten Knoten entfernt, existieren danach nur zwei Komponenten mit den Knoten {d} und {e, f} (analog beim Entfernen der blauen Knoten). Aus diesem Graph kann man einen K5-Minor formen, indem z.B. die Knoten d und c verschmolzen werden.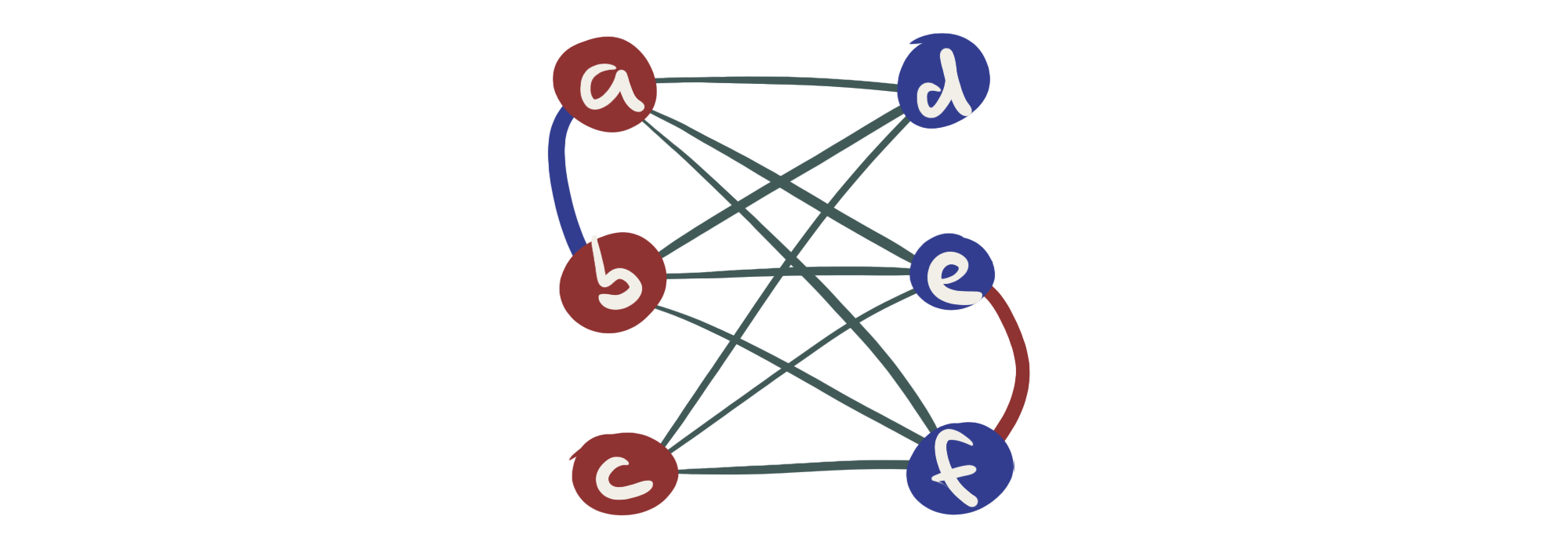
Wir wissen jetzt, wie wir K3,3-Minoren bei der Planaritätsprüfung behandeln können, müssen allerdings die beiden Ausnahmen beachten:
- Der K3,3-Minor ist Teil eines K5-Minors. Teilen wir den Graph entlang des K3,3s in augmentierte Komponenten, machen wir ggf. genau diesen K5-Minor kaputt. Also suchen wir nach ein paar zusätzlichen Pfaden außerhalb des K3,3-Minors, um das zu prüfen. Hier gibt es eine Menge an verschiedenen Fällen, die wir uns nicht alle einzeln anschauen werden - das Grundprinzip ist das aus Abb. 7.
- Der Graph ist eine Art Rad mit 8 Knoten (s. Abb. 8). Dieser spezielle Graph wird W genannt und ist eine Sackgasse für unseren Algorithmus. Auf ihn treffen zwar die Bedingungen für das Aufteilen in augmentierte Komponenten zu, allerdings enthält W zu wenig Pfade dafür. Aber W enthält auch keinen K5-Minor also können wir unseren Algorithmus hier stoppen.
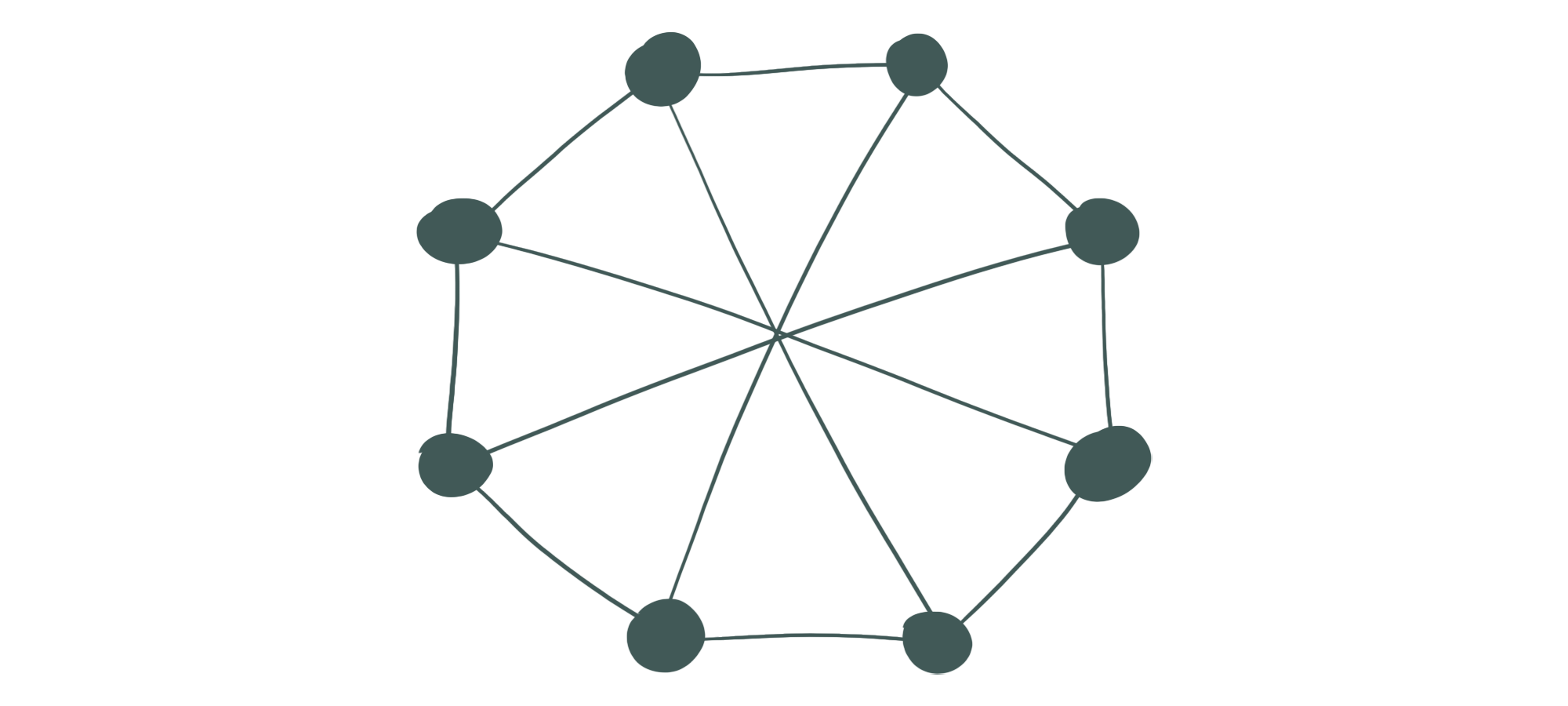
Abb. 8: Der Graph W
Langsam wird es kompliziert…denn zu den beiden Ausnahmen (und dem gesamten Algorithmus) sei erwähnt, dass wir ihn nur auf 3-zusammenhängenden Graphen ausführen. D.h. dass wir 2 beliebige Knoten aus unserem Graph entfernen können und er danach immer noch zusammenhängend ist.
Ist der Graph z.B. nur 2-zusammenhängend, gibt es mindestens ein Knotenpaar, dass wir entfernen können, sodass der Graph in mehrere getrennte Komponenten zerfällt.
Solche Knoten werden als 2-Separator bezeichnet, weil es 2 Knoten sind und sie bei Entfernen den Graph separieren:
Abb. 9: Ein 2-zusammenhängender Graph mit dem 2-Separator {a, b}.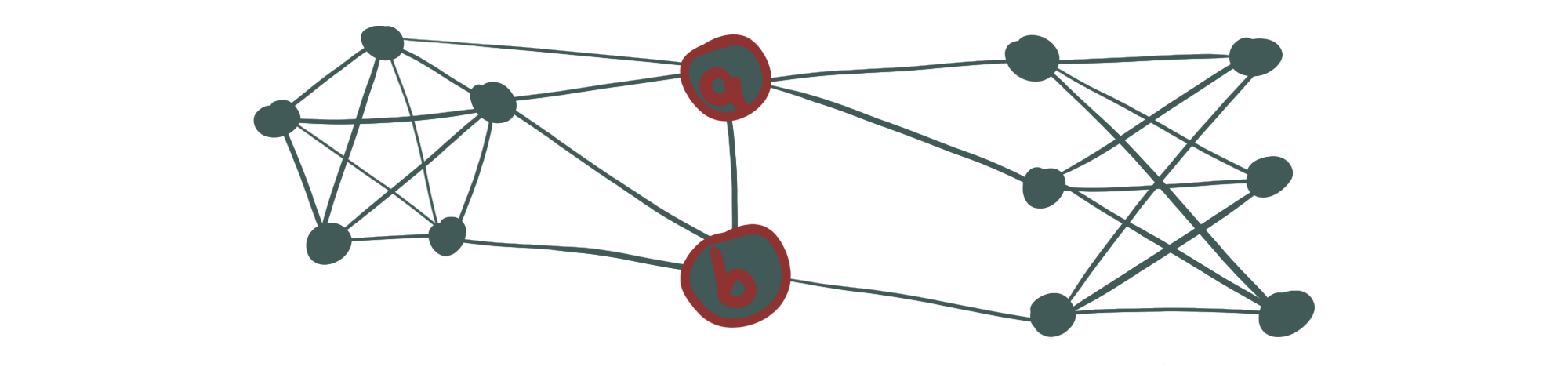
Sequenzieller Algorithmus zum Finden von K5-Minoren
Hier eine Zusammenfassung, wie der Algorithmus auf einem Graph G arbeitet:
- Gibt es einen 1-Separator in G, dann bilde damit augmentierte Komponenten und wende den Algorithmus rekursiv auf jede an.
- Gibt es einen 2-Separator in G, dann bilde damit augmentierte Komponenten und wende den Algorithmus rekursiv auf jede an.
- Planaritätstest:
- G ist planar: Gib zurück, dass kein K5-Minor enthalten ist.
- G enthält einen K5-Minor: Gib den K5-Minor zurück und beende den Algorithmus.
- G enthält einen K3,3-Minor: Weiter zu Schritt 4
- G ist W: Gib zurück, dass kein K5-Minor gefunden wurde. Andernfalls weiter zu Schritt 5
- Wenn die roten Knoten einen 3-Separator bilden, sodass die blauen Knoten in jeweils eigenen Komponenten liegen, können wir daraus augmentierte Komponenten erzeugen und den Algorithmus ab Schritt 3 rekursiv auf diese Komponenten anwenden. (Analog für die blauen Knoten als 3-Separator)
- Ist dieser Schritt erreicht, enthält G einen K5-Minor bestehend aus dem K3,3-Minor und dem Pfad, der zwei rote, sowie dem Pfad, der zwei blaue Knoten verbindet.